Lecture note Nr.3

Nr. 017

I would reccomend a quiet interesting page with the basics geomety shapes in dinamic figures. Let s have a look!
http://tfeind.bprmedia.hu/webre/Tartalom.htm

Representation of circle

Nr. 016

Represent a circle in Monge throught the following problem:

There is P point and t=XY line and T pont on it. Construct a circle passing throught P point and t is a tangent in T point. Show the main diameters of the circle and the tangent of them. P(45, 70, 235); X(45, 100, 275); T(100, --, --); Y(200, 150, 205).

The solution of the construction:
http://hasznosdoksik.hu/geo/korszerkesztes.pdf

Intersection of two prism

Nr. 015

Let's see an intersection of two polohedrons.

Click for the solution:

http://hasznosdoksik.hu/geo/athatas.pdf

Metrical construction of a prism

Nr. 014.

Construct a right prism with regular pentagon base. See the task and the solution here:

http://hasznosdoksik.hu/geo/hasab_6oldalu.pdf

Intersection of a plane and a sphere

Nr. 013.

Here a 3D picture of the solution of the intersection. If you remove the plane from your sphere it might look like this:

Let's see the whole problem in Monge:
http://hasznosdoksik.hu/geo/gomb_sik.pdf

Intersection of a pair of plane sheets

Nr. 012

Construct the intersection of a pair of plane sheets and show the shadow as well. In this problem you can see the construction of transversal, intersection of 2 planes and shadows.

Follow the solution in the link below:
http://hasznosdoksik.hu/geo/sikmetszes_tranzverzalis.pdf

Construct a prism

Nr. 011

New problem from also BME facuty of Mechanical Engeneer. We need to construct a prosm from the given one of the base line and an edge.

See the solution here:
http://hasznosdoksik.hu/geo/testepites_hasab.pdf

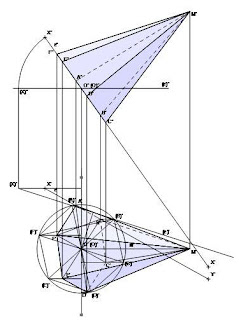
Polyhedron construction (pyramid)

Nr. 010

I found a homework from a faculty of Mechanical Engeneer of BME homepage. Let's see the problem:
Construct a right pyramid with base hexagonal ABCDEF square. The A and B points are laying on the e=XY line, the base circle is given by O, witch is laying down on the secondprojeting plane of e. The height of the polyhedron is m. Choose the right side of the solutions. Show the visibility. X(30,115, 240); Y(165, 40, 50); O(60, 65, -); m=110

Here the construction step by step:
http://hasznosdoksik.hu/geo/gula_epites_.pdf

Transversal 3. (normal transversal)

Nr. 009
Special transversal is perpendicular to the skews lines.
Here the steps to the construction:
http://hasznosdoksik.hu/geo/tranzverzalis_normal.pdf

Transversal 2. (paralell with a direction)

Nr. 008
Second part is to draw a transversal paralell with a direction between two skew lines.

http://hasznosdoksik.hu/geo/tranzverzalis_irannyal.pdf